Kruskal-Wallis Test

I want to mentally prepare for the upcoming semester. Today, let me do a warm-up exercise of computing a Kruskal-Wallis test.

library("palmerpenguins")
library("tidyverse")

You can see that I will use the ubiquitous Palmer Penguins data set

str(penguins)

## tibble [344 × 8] (S3: tbl_df/tbl/data.frame)
##  $ species          : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
##  $ island           : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
##  $ bill_length_mm   : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...
##  $ bill_depth_mm    : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...
##  $ flipper_length_mm: int [1:344] 181 186 195 NA 193 190 181 195 193 190 ...
##  $ body_mass_g      : int [1:344] 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...
##  $ sex              : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...
##  $ year             : int [1:344] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...

Our null hypothesis will be that the three species of penguins have the same bill length. Let us first get a visual.

penguins |>
  ggplot() +
  geom_boxplot(aes(x = species, y = bill_length_mm,
                   fill = species)) +
  labs(title = "Palmer Penguins",
       subtitle = "null hypothesis: the three species of penguins have the *same* bill length",
       caption = "Derek Sollberger") +
  theme_minimal()

## Warning: Removed 2 rows containing non-finite values (stat_boxplot).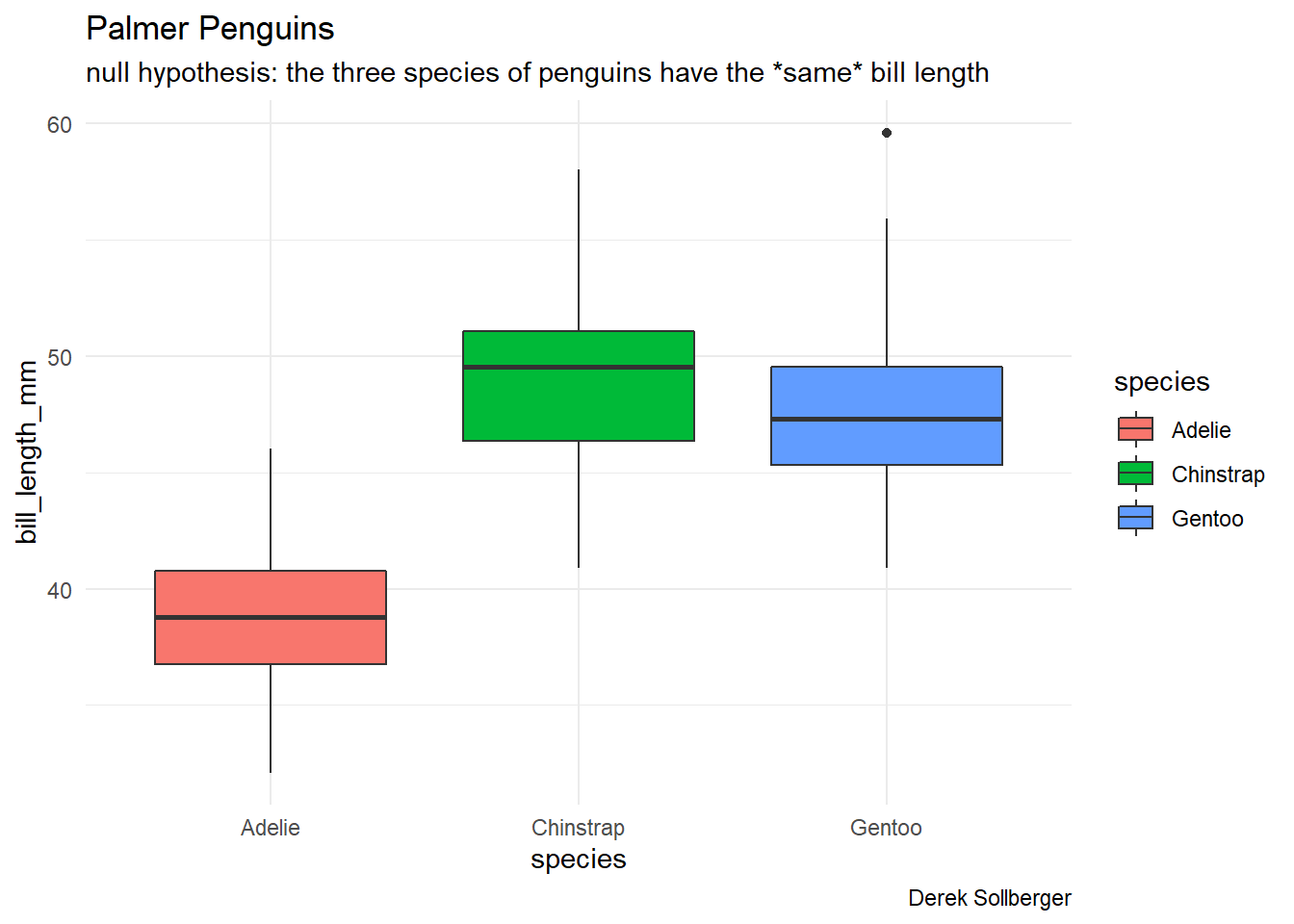

Visually, it appears that the penguins tend to have different bill lengths. To be more scientifically sound, let us now run the Kruskal-Wallis test.

# https://datasciencetut.com/how-to-perform-the-kruskal-wallis-test-in-r/
kruskal.test(bill_length_mm ~ species, data = penguins)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  bill_length_mm by species
## Kruskal-Wallis chi-squared = 244.14, df = 2, p-value < 2.2e-16

Since the p-value is less than 0.05, let us reject the null hypothesis of equal bill lengths.

===

The blog post mentioned above also told of a way to do pairwise comparisons in this setting (i.e. more than 2 labels)

pairwise.wilcox.test(penguins$bill_length_mm, penguins$species,
                     p.adjust.method = "BH")

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  penguins$bill_length_mm and penguins$species 
## 
##           Adelie Chinstrap
## Chinstrap <2e-16 -        
## Gentoo    <2e-16 0.0018   
## 
## P value adjustment method: BH

In this quick example, it appears that, pairwise, each species bill length is significally different than the other species.